计算机组成原理

第一节计算机系统层次结构

1.计算机系统的基本组成：硬件+软件

2.计算机硬件的基本组成：运算器+存储器+控制器+输入设备+输出设备

3.系统软件和应用软件

系统软件	操作系统、数据库管理系统、语言处理程序、分布式软件系统、网络软件系统、标准库语言、服务性程序
应用软件	科学计算类程序、工程设计类程序、数据统计与处理程序

4.（易考）翻译程序：

汇编程序（汇编器）	将汇编语言程序翻译成机器语言程序
解释程序（解释器）	将源程序翻译成机器指令并立即执行
编译程序（编译器）	将高级语言翻译城机器语言或汇编语言

第二节计算机性能指标

吞吐量：表征一台计算机在某一时间间隔内能够处理的信息量。
响应时间：表征从输入有效到系统产生响应之间的时间度量，用时间单位来度量。
利用率：在给定的时间间隔系统被实际使用的时间所占的比率，用百分比表示。
处理机字长：指处理机运算器中一次能够完成二进制数运算的位数，如 32 位、64 位。
总线宽度：一般指 CPU 中运算器与存储器之间进行互连的内部总线二进制位数。
存储器容量：存储器中所有存储单元的总数目，通常用 KB、MB、GB、TB 来表示。公式一般是：位数×个数

（MAR×MDR）

存储器带宽：单位时间内从存储器读出的二进制数信息量，一般用字节数/秒表示。
主频/时钟周期：CPU 的工作节拍受主时钟控制，主时钟不断产生固定频率的时钟度量单位是 MHz、GHz

主频的倒数称为 CPU 时钟周期（T），T=1/f，度量单位是 μs、ns。

K= 103 ，M= 106 ，G= 109

易错：时钟频率的提高，不能保证CPU执行速度又同倍速的提高，有时候还会减慢。

CPU 执行时间：表示 CPU 执行一般程序所占用的 CPU 时间，可用下式计算：

CPU 执行时间 = CPU 时钟周期数 * CPU 时钟周期

CPI：执行一条指令所需的平均时钟周期数。用下式计算：

CPI = 执行某段程序所需的 CPU 时钟周期数 / 程序包含的指令条数

MIPS：（Million Instructions Per Second）的缩写，表示平均每秒执行多少百万条定点指令数，用下式计算：

MIPS = 指令数 / （程序执行时间 * 10^6）

FLOPS：（Floating-point Operations Per Second）的缩写，表示每秒执行浮点操作的次数，用来衡量机器浮点操作的性能。用下式计算：FLOPS = 程序中的浮点操作次数 / 程序执行时间（s）

题目总结：

①对于高级语言程序员来说，浮点数格式、乘法指令、数据如何在运算器中运算时透明的。对于汇编语言程序员，指令格式，机器构造，数据格式则不是透明的。

②在CPU中，IR、MAR、MDR对各类程序员都是透明的。

③机器字长，指令字长，存储字长

机器字长也称字长——是计算机直接处理二进制数据的位数，机器字长一半等于内部寄存器的大小，它决定了计算机的运算精度。

指令字长——一个指令中包含的二进制代码的位数。

存储字长——一个存储单元中二进制代码的长度。

指令字长一般是存储字长的整数倍，若指令字长等于存储字长的2倍，则需要2次访存来取出一条指令，因此取值周期为机器周期的2倍；若指令字长等于存储字长，则取值周期等于机器周期。

第二章数据的表示和运算

一、无符号整数的表示和运算

Ⅰ、无符号整数的加法：从最低位开始，按位相加，并往更高位进位。

Ⅱ、”被减数“不变，”减数“全部按位取反，末位+1，减法变加法。

二、带符号整数的表示和运算

带符号的整数表示：原码、补码、反码

※带符号的整数运算可以用原码吗？

用原码的话符号位不能参与运算，需要设计复杂的硬件电路才能处理，贵。

这时候就可以利用补码来进行带符号的整数运算。

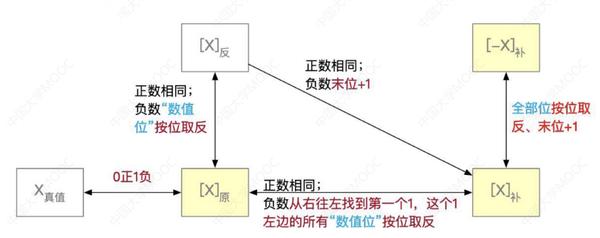
①涉及原码和补码的转化。

正数：原码->补码，不变

负数：原码->补码，除符号位外，各位取反，末位+1

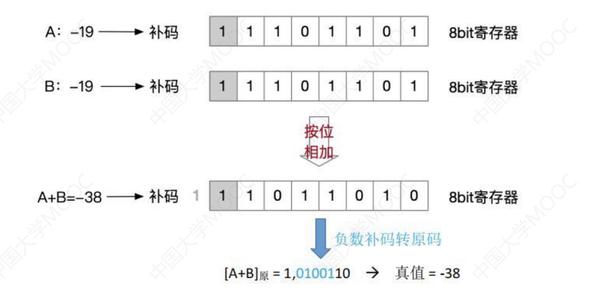
Ⅰ、补码的加法

从最低位开始，然后按位相加，并往高位进位。算出来的结果，转回原码，就可以得到正值。

补充：补码->原码：类似，除符号位外，各位取反，末位+1

Ⅱ、补码的减法

※加法电路造价便宜，减法电路造价昂贵，若将减法变为加法，更加economize。

那我们知道了”减数“的补码，那如何求得”减数“负值的补码呢？

补码全部位取反，末位+1（易错这里是全部位取反，而带符号位的负数，是除符号位外，各位取反）

其实啊，这里的运算的逻辑结构和无符号的减法运算是一样的，通用一套电路，省钱！

三、原码、反码和补码的特性对比

8bit	合法的表示范围	最大的数	最小的数	真值0的表示
带符号原码	-127~127	127	-127	+0=00000000 -0=10000000
带符号反码	-127~127	127	-127	+0=00000000 -0=11111111
带符号补码	-128~127	127	-128	-/+0=00000000 只有这一种
无符号整数	0~255	255	0	00000000
带符号移码	-128~127	127	-128	0=10000000 只有这一种

原码和反码的合法表示范围完全相同，而且都有两种表示真值0的方法。

补码的合法表示范围多一个负数，原因就是只有一种0的表示方法，因为-0的补码就是00000000

四、移码，定点小数

移码：在补码的基础上符号位取反。且移码只能表示整数。表示范围和补码相同。

移码的作用：移码的作用就是方便计算机比较两个数数值的大小。

定点小数的编码表示：原码、反码、补码。

运算规则和整数的运算规则一模一样。

五、电路的基本原理和加法器设计

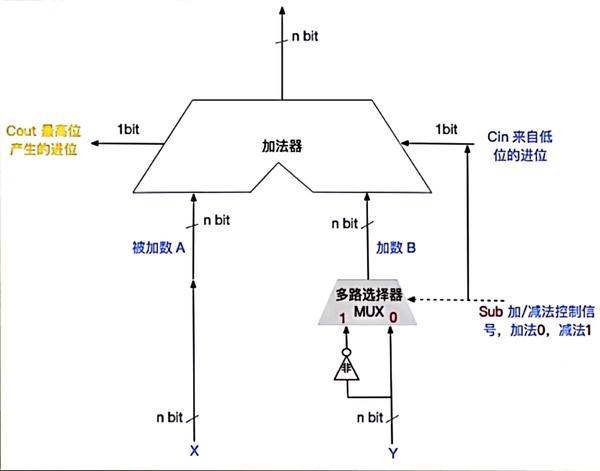
Ⅰ、补码/无符号整数加减法运算器

减法运算过程：

①首先Sub信号置为1；

②多路选择器的值为1，Y（减数）经过非门，都取反；

③cin来自低位加1；

Ⅱ、标志位生成

①进位标志CF (Carry Flag)只对无符号运算有意义
当运算结果的最高有效位有进位（加法）或借位（减法）时，进位标志置1，

即CF = 1；否则CF= 0。

49H + 6DH＝B6H，　没有进位：CF = 0

BBH + 6AH＝（1）25H，有进位：CF = 1

②零标志ZF (Zero Flag)
若运算结果为0，则ZF = 1；否则ZF = 0

49H + 6DH＝B6H，结果不是零：ZF = 0

75H + 8BH＝（1）00H，结果是零：ZF = 1

③符号标志SF (Sign Flag)只对有符号运算有意义
运算结果最高位为1，则SF = 1；否则SF = 0

49H + 6DH＝B6H=10110110B，SF=1

④溢出标志OF (Overflow Flag)只对有符号运算有意义
若算术运算的结果有溢出，则OF＝1；否则 OF＝0

49H + 6DH ＝B6H，产生溢出：OF = 1

75H + 8BH ＝（1）26H，没有溢出：OF = 0

进位CF和溢出OF位有什么区别呢？

进位标志表示无符号数运算结果是否超出范围，运算结果仍然正确，对有符号位加减法无意义。

溢出标志表示有符号数运算结果是否超出范围，运算结果已经不正确，对无符号加减无意义。

溢出的判断判断运算结果是否溢出有一个简单的规则：

只有当两个相同符号数相加（包括不同符号数相减），而运算结果的符号与原数据符号相反时，产生溢出；因为，此时的运算结果显然不正确其他情况下，则不会产生溢出

1.当两个符号相同的数相加，结果的符号与之相反，则OF=1,否则OF=0.

2.当两个符号不同的数相减，结果的符号与减数相同，则OF=1,否则OF=0.

六、定点数的移位运算

左移1位相当于×2，右移1位相当于÷2
原码：符号位不参与移位。左移，右移都补0
反码：符号位不参与移位。若反码是负数补1；若反码是正数补0
补码：符号位不参与移位。若补码是负数左移低位补0，右移高位补1；若补码是正数，左移右移都补0

七、原码补码的乘法除法运算

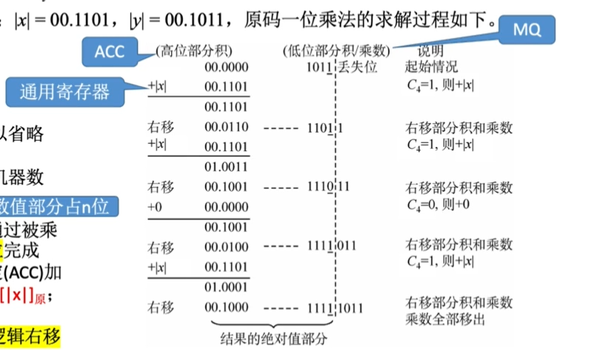
Ⅰ、原码的一位乘法

符号位通过异或确定；数值部分通过被乘数和乘数绝对值的n轮加法、移位完成，根据当前乘数中参与运算的位确定（ACC）加什么。若当运算位=1，则（ACC）+[|x|],若为0，则(ACC)+1。每轮加法完成后，ACC,MQ的内容统一逻辑右移。

先ACC初始化。x置于通用寄存器中，y置于MQ。

Ⅱ、补码的一位乘法

原码一位乘法和补码一位乘法的不同点

原码一位乘法	补码一位乘法
进行n轮的加法、移位	进行n轮加法，移位，最后再多来一次加法
每次加法相加，只有两种情况+0或加x	每次加法加有三种情况，0或+x或+[-x]
每次移位都是逻辑右移，补1	每次都是补码的右移，正数右移补0，负数右移补1
符号位不参与运算	符号位参与运算

会添加一位辅助位
辅助位-MQ中“最低位”=1时，(ACC)+[X)]补
辅助位-MQ中“最低位”=0时，(ACC)+0
辅助位-MQ中“最低位”=-1时，(ACC)+[-X]补

八、C语言类型转换和数据存储排列

C语言中定点整数是用”补码“存储的。
无符号数转为有符号数：不改变数据内容，改变解释方式。
长整数变为短整数：高位截断，保留低位。
短整数变长整数：若为有符号数，在符号位和数值位添1，若为无符号，直接在高位添0。
大小端模式：大端方式便于人类阅读；小段方式便于机器处理，因为机器最先读入的就是最应被处理的数据。
边界对齐：假设存储字长为32位，则1个字=32bit,半字=16bit。每次访存只能读/写1个字。若采用边界对齐的方式，则访问一个字/半字都需要一次访存，虽然会造成一点点的空间浪费。采用不对齐的方式，对空间利用率高，但是可能会涉及到两次访存时间大大增加。

九、浮点数的表示和运算

Ⅰ、概念：之前我们学习了定点数，其中「定点」指的是约定小数点位置固定不变。那浮点数的「浮点」就是指，其小数点的位置是可以是漂浮不定的。

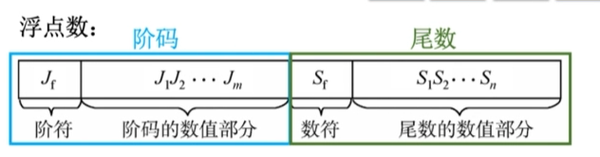
Ⅱ、表示：阶符表示的是阶码正负，尾数的数符表示的是尾数正负。

阶码：常用补码或移码表示的定点整数，反映表示范围。

尾数：常用原码或补码表示的定点小数，反映精度。

Ⅲ、规格化：规定尾数的最高位必须是有效位。

①”有效位“又分两种情况。分为尾数是补码表示还是原码表示

原码表示的尾数视格化：尾数的最高数值位必须是1

补码表示的尾数规格化：尾数最高数值位必须和尾数符号位相反

②左规：当浮点数运算的结果为非规格化时要进行规格化处理，将尾数算数左移一位，阶码减1。

b= 22×(+0.01001)=21×(+0.10010) #尾数最高位为0，左规

右规：当浮点数运算的结果尾数出现溢出（双符号位为01或10）时，将尾数算数右移一位，阶码加1。

采用双符号位，当发生溢出时（双符号位为01或10），可以采用右规，更高位的符号位是正确的符号位。

③虽然浮点数的范围和精度也有限，但其范围和精度都已非常之大，所以在计算机中，对于小数的表示我们通常会使用浮点数来存储。

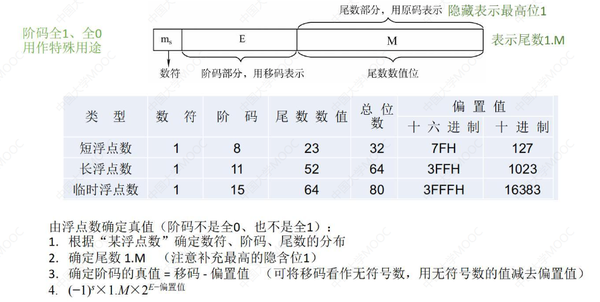
十、IEEE 754

背景：在浮点数提出的早期，各个计算机厂商各自制定自己的浮点数规则，导致不同厂商对于同一个数字的浮点数表示各不相同，在计算时还需要先进行转换才能进行计算。后来 IEEE 组织提出了浮点数的标准，统一了浮点数的格式，并规定了单精度浮点数 float 和双精度浮点数 double，从此以后各个计算机厂商统一了浮点数的格式，一直延续至今。